
Speed Sudoku - Play web sudoku puzzle games online for free!
Instructions - Sudoku Techniques
The Lingo
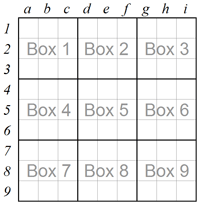
Sudoku grid consists of 81 squares divided into nine columns marked a through i, and nine rows marked 1 through 9. The grid is also divided into nine 3x3 sub-grids named boxes which are marked box 1 through box 9.
Scanning techniques
The easiest way starting a Sudoku puzzle is to scan rows and columns within each triple-box area, eliminating numbers or squares and finding situations where only a single number can fit into a single square. The scanning technique is fast and usually sufficient to solve easy puzzles all the way to the end. The scanning technique is also very useful for hard puzzles up to the point where no further progress can be made and more advanced solving techniques are required. Here are some ways of using scanning techniques:
1. Scanning in one direction:
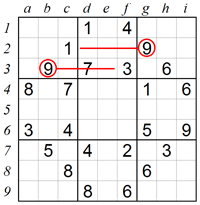
In our first example we will focus on box 2, which like any other box in Sudoku must contain 9. Looking at box 1 and box 3 we can see there are already 9s in row 2 and in row 3, which excludes the two bottom rows of box 2 from having 9. This leaves square e1 as the only possible place into which 9 can fit in.
2. Scanning in two directions:
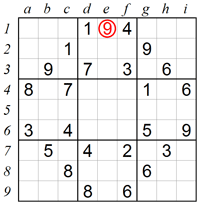
The same technique can be expanded by using information from perpendicular rows and columns. Let’s see where we can place 1 in box 3. In this example, row 1 and row 2 contain 1s, which leaves two empty squares in the bottom of box 3. However, square g4 also contains 1, so no additional 1 is allowed in column g. This means that square i3 is the only place left for 1.
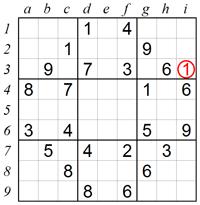
3. Searching for Single Candidates:
Often only one number can be in a square because the remaining eight are already used in the relevant row, column and box. Taking a careful look at square b4 we can see that 3, 4, 7 and 8 are already used in the same box, 1 and 6 are used in the same row, and 5 and 9 are used in the same column. Eliminating all the above numbers leaves 2 as the single candidate for square b4.
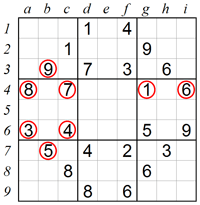
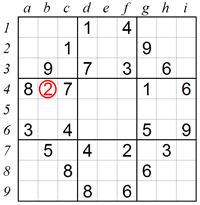
4. Eliminating numbers from rows, columns and boxes:
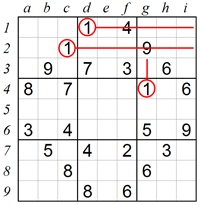
There are more complex ways to find numbers by using the process of elimination. In this example the 1 in square c8 implies that either square e7 or square e9 must contain 1. Whichever the case may be, the 1 of column e is in box 8 and it is therefore not possible to have 1 in the centre column of box 2. So the only square left for 1 in box 2 is square d2.
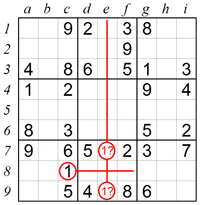
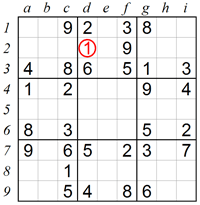
5. Searching for missing numbers in rows and columns:
This method can be particularly useful when rows (and columns) are close to completion. Let’s take a look at row 6. Seven of the nine squares contain the numbers 1, 2, 3, 4, 5, 8 and 9, which means that 6 and 7 are missing. However, 6 cannot be in square h6 because there is already 6 in that column. Therefore the 6 must be in square b6.
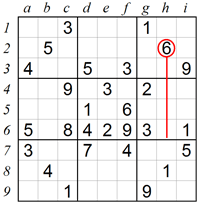
Analyzing techniques
As Sudoku puzzle levels get harder you will find the simple scanning methods described above are not enough and more sophisticated solving techniques must be used. Hard puzzles require deeper logic analysis which is done with the aid of pencilmarks. Sudoku pencilmarking is a systematic process writing small numbers inside the squares to denote which ones may fit in. After pencilmarking the puzzle, the solver must analyze the results, identify special number combinations and deduce which numbers should be placed where. Here are some ways of using analyzing techniques:
1. Eliminating squares using Naked Pairs in a box:
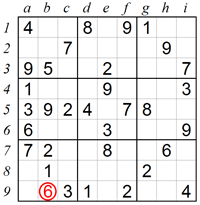
In this example, squares c7 and c8 in box 7 can only contain 4 and 9 as shown with the red pencilmarks below. We don’t know which is which, but we do know that both squares are occupied. In addition, square a6 excludes 6 from being in the left column of box 7. As a result the 6 can only be in square b9. Such cases where the same pair can only be placed in two boxes is called Disjoint Subsets, and if the Disjoint Subsets are easy to see then they are called Naked Pairs.
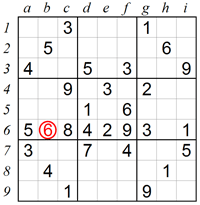
2. Eliminating squares using Naked Pairs in rows and columns:
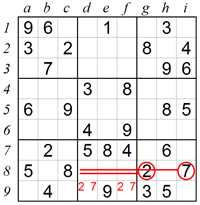
The previous solving technique is useful for deducing a number within a row or column instead of a box. In this example we see that squares d9 and f9 in box 8 can only contain 2 and 7. Again we don’t know which is which, but we do know that both squares are occupied. The numbers which remain to be placed in row 9 are 1, 6 and 8. However, 6 can’t be placed in square a9 or in square i9, so the only possible place is square c9.
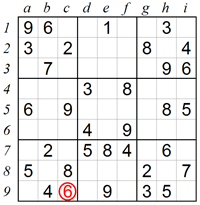
3. Eliminating squares using Hidden Pairs in rows and columns:
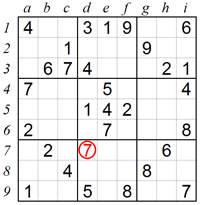
Disjoint Subsets are not always obvious to see at first sight, in which case they are called Hidden Pairs. If we take a very close look at the pencilmarks in row 7 we can see that both 1 and 4 can only be in square f7 and square g7. This means that 1 and 4 are a Hidden Pair, and that square f7 and square g7 cannot contain any other number. Using the scanning technique we see that 7 can only be in square d7.
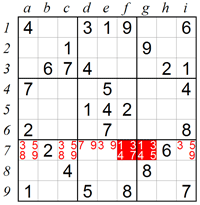
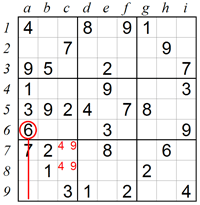
4. Eliminating squares using X-Wing:
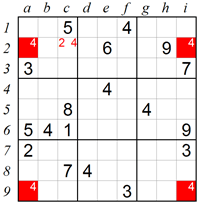
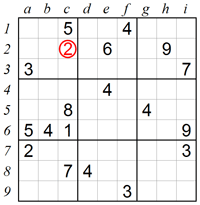
The X-Wing technique is used in rare situations which occur in some extremely difficult puzzles. Scanning column a we see that 4 can only be in square a2 or square a9. Similarly, 4 can only be in square i2 or square i9. Because of the X-Wing pattern where boxes are in the same row (or column), a new logic constraint occurs: it is obvious that in row 2 the 4 can only be either in square a2 or in square i2, and it cannot be in any other square. Therefore 4 is excluded from square c2, and square c2 must be 2.
Copyright © 1997-2009 Conceptis Ltd. Used with permission.
Headlines
Fri Feb 14, 2014 9:54 pm
[Server]
The Future of Speed Sudoku
Tue May 29, 2012 3:00 pm
[Features]
Medals
Fri May 25, 2012 9:34 am
[Features]
Chat before entering game
Thu May 10, 2012 11:34 am
[Features]
New server, annual premium membership
Mon May 24, 2010 7:53 pm
[Community]
Web Developer appointed
Wed Jan 06, 2010 5:02 pm
[Server]
The game is working again
Thu Sep 17, 2009 3:46 pm
[Server]
New Server
Sun Jun 28, 2009 8:51 pm
[Community]
Live Chat with Caedda - June 30, Noon CDT
Wed May 27, 2009 7:14 pm
[Community]
Live Chat With Caedda - May 28, 2:00 PM CDT